11 Dose-Response Modelling; Why We Need Integrated Analyses Across All Doses/Trials
At the end of this chapter, the reader will understand:
Why we must always “think” and “act” based on integrated analyses across all doses/trials.
Why we need suitable designs and D-E-R models to fully understand the shape of the D-E-R relationships.
Why interpreting observed outcomes at a specific dose level is naïve, can be misleading, and is never scientifically justified when we have data from multiple dose levels.
Why investigating narrow dose ranges in few individuals is never an acceptable “dose- ranging” trial.
That dose-ranging trials need to be prospectively simulated to understand their ability to accurately and precisely quantify the true D-E-R relationships. To simply collect data from a few doses and “hope” for a clear understanding of the D-E-R relationships is unethical.
Fundamentally, if we wish to understand how changes in dose (say from 10 mg to 15 mg) will lead to changes in response, we need to understand the shape of the dose-response relationship. I often see D-R data being poorly analysed and interpreted. For example, imagine a “dose-ranging” trial considered three doses of 9 mg, 10 mg and 11 mg. Some hypothetical results are shown in Table 11.1 below (this could be an oncology trial, where Efficacy is Overall Survival and Safety is a Grade ≥ 3 toxicity).
| Dose | Efficacy | Safety |
|---|---|---|
| 9 mg | 30% (3/10) | 10% (1/10) |
| 10 mg | 60% (6/10) | 10% (1/10) |
| 11 mg | 60% (6/10) | 40% (4/10) |
Given the above data, a naïve person may conclude 10 mg is the “sweet spot”, yielding the best efficacy/safety trade-off, since the observed efficacy at 9 mg is inferior to the higher doses, whilst the observed safety at 11 mg is inferior to the lower doses. It seems that 10 mg has truly the best overall profile, but this is wrong. We need to think about the cascade from dose to PK to PD; we need to understand the science. This range of doses would yield near identical (and overlapping) exposure ranges across individuals, and hence the true PD effects would be near identical for each of the doses. That is, our best point estimate for Efficacy should be close to 50% (15/30) and close to 20% (6/30) for Safety for all doses. Had we actually seen this in a clinical trial, these observed results are just one realisation when we “toss a coin” with true response rates for efficacy at some value around 50%, and for safety with a true response rate around 20%; the 10 mg arm just happened to “get lucky”, with the 10 individuals at 10 mg yielding, by chance, the most favourable (observed) outcomes.
The above example is extreme in that the dose range chosen (9-11mg) is very narrow, but it clearly highlights one common error seen in drug development, that of naively selecting phase 3 doses based on observed outcomes from small phase 2 trials with very limited dose ranges. In the above example, whilst the pharmaceutical company may expect the 10 mg dose to yield a 60% response for efficacy and 10% response rate for safety in the larger phase 3 trials, in actuality these would be nearer 50% and 20% from the integrated analysis using all dose levels. If we were to imagine that a control arm in phase 3 might yield a 40% response rate, then the pharmaceutical company may design their phase 3 trials assuming a 20% treatment difference (60%-40%) rather than a 10% treatment difference (50%-40%). To achieve 90% power to show a 10% difference required 4 times the sample size compared with a 20% difference. Hence their phase 3 trial would be both underpowered to demonstrate superiority and very unlikely to yield an observed treatment difference anywhere near the 20% that they had expected/hoped for. The pharmaceutical company has over-estimated the expected response rate in phase 3 by ignoring any form of integrated dose-response modelling and the science that underpins the relationships between dose, exposure and response. Worse still, had similar results come from a phase 3 trial that investigated closely spaced dose levels, both the pharmaceutical company and regulator may be misled on the actual true response rates across the dose range for both efficacy and safety.
This example shows that it is always dangerous to focus on the observed outcomes for individual dose levels; rather we should always look to combine data across all doses (and trials) to fully understand the D-R relationships. To achieve this, we always need to analysis all data from all doses/trials simultaneously, and utilise a suitable D-R model.
Although experienced drug developers/regulators may think that they would never interpret the above table so naively, consider the following results in Table 11.2
| Dose | Efficacy | Safety |
|---|---|---|
| 5 mg | 30% (3/10) | 10% (1/10) |
| 10 mg | 60% (6/10) | 10% (1/10) |
| 15 mg | 60% (6/10) | 40% (4/10) |
Here, I have simply changed the doses from 9-11 mg to 5-15 mg. I make this point based on a recent FDA discussion on Project Optimus, where the dosing regimen for idelalisib (brand name Zydelig) was discussed. The discussion centered on how the approved 150 mg bid dose was now considered too high. The discussant then showed a table with efficacy and safety results based on doses from 50 mg qd to 350 mg bid. The results were based on a small N for each dose regimen, and hence were not very dissimilar to the above. Based on the observed safety data at 100 mg bid looking numerically much better than that at 150 mg bid, one participant suggested that 100 mg bid could be a much better/safer (optimal?) dose than 150 mg bid. Is this suggestion sound?
From the FDA label, we can better understand some key information about the relationship between dose and exposure for idelalisib (my emphasis):
“Idelalisib exposure increased in a less than dose-proportional manner over a dose range of 50 mg to 350 mg twice daily in the fasted state.”
When we have dose proportionality, we expect the exposures at 100 mg bid to be, on average, 67% of those at 150 mg bid (67% = 100/150). However the above suggests that the exposures at the 100 mg bid are likely to be closer to the exposures at 150 mg bid. The IIV in clearance for idelalisib (directly related to IIV in exposure) is quoted as 38.6% [1], the typical exposure (measured by AUC) is quoted as 10010 ng.h/mL, and we can (conservatively) approximate that the exposures at 100 mg bid are likely to be nearer 75% of the exposures at 150 mg bid (they may be even closer, and the IIV even higher, but these ballpark figures will suffice to make the point here). Figure 11.1 shows the distributions of exposures (as measured by AUC) for 150 mg bid in the two top panels (these are identical except for random sampling differences across 10000 simulated patients). The bottom panels show the distribution of exposures when we use the Not Proportional estimate (75%) and the Dose Proportional (67%) value for 100 mg bid.
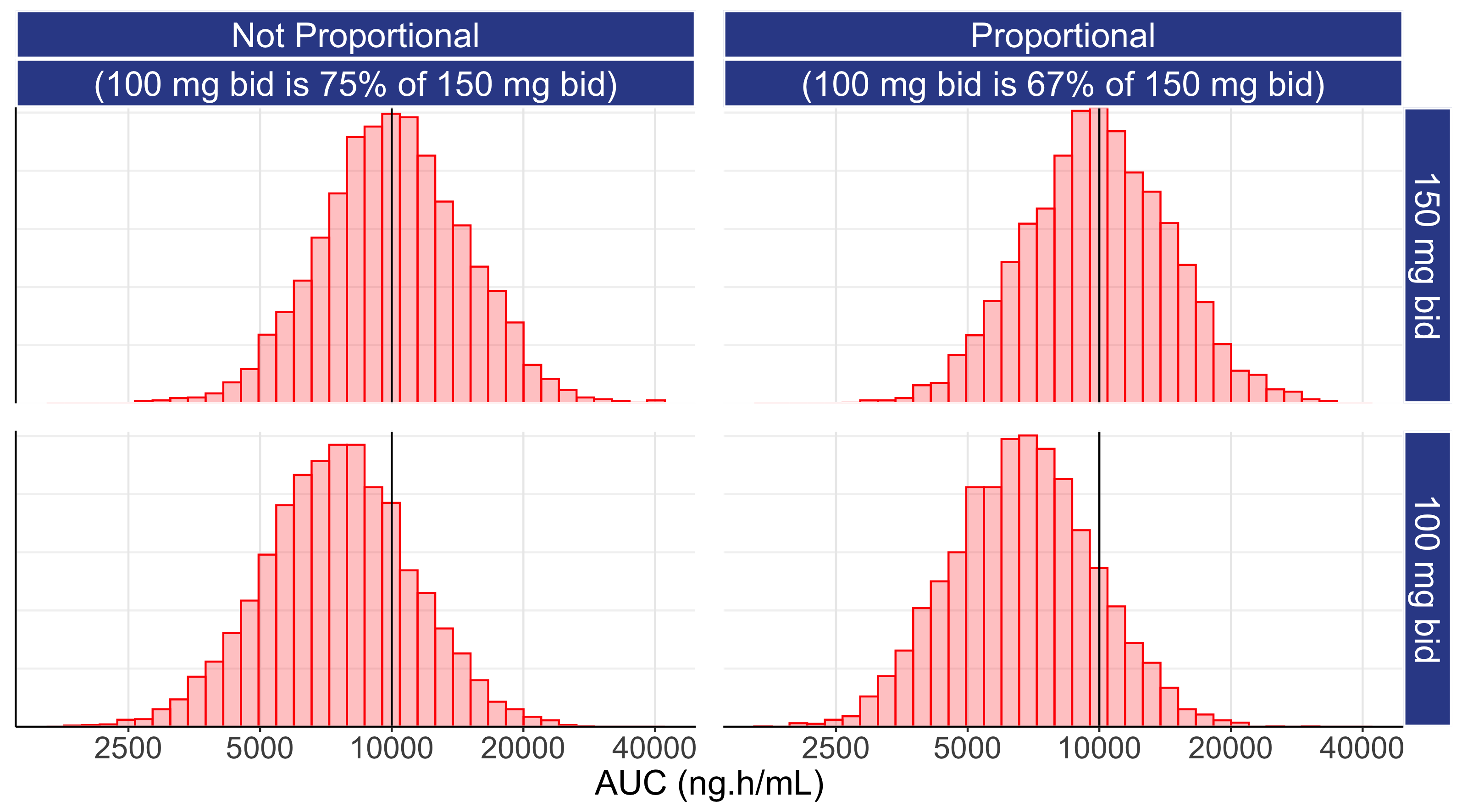
Under both the Not Proportional and Proportional scenarios, the distributions of exposures significantly overlap across the two dose levels. Recall that when the distributions of PK exposures overlap, the PD effects will be similar (even if we tried here to foolishly use a step function for the exposure response relationship). Thus purely on understanding the IIV for a drug, how close the two dose levels are, and by understanding that exposure response relationships for PD do not follow step functions, we can make informed observations about the relative effects of these two doses.
Returning to the above table for our fictitious drug/trial, our 15 mg dose is 50% higher than 10 mg (i.e. similar to the ratio of 150 mg bid to 100 mg bid with idelalisib). Thus for our fictitious drug (or idelalisib), is it possible that the D-E-R is very steep, and 10 mg (100 mg bid) is quite safe, when 15 mg (150 mg bid) is not?
In short, no, science tells us that this is not possible.
If the 150 mg bid dose of idelalisib was found in later phase 3 trials to have a poor safety profile, the safety profile at 100 mg bid would not be “clean”.
D-E-R relationships do not follow “step functions” where we suddenly go from no effect to a much larger effect.
In addition, when doses are close with overlapping exposure ranges, we can be confident that the safety profiles of the two doses will not be very different. Thus although idelalisib 100 mg bid may well have a better safety profile compared with 150 mg bid, we can only accurately quantify these differences from well conducted trials using very wide dose ranges, sufficiently large sample sizes and appropriate D-E-R modelling incorporating all doses/trials. Simply”eye-balling” the observed data for each dose is neither a scientific nor reliable method for any form of (accurate) dose selection.
To conclude the discussion around the results for our fictitious drug trial, we cannot accurately or precisely determine the D-R for either efficacy or safety from such a weak design; the dose range is far too narrow and the sample size is far too small. When faced with such limited data from such an awful trial design, companies /teams /regulators /individuals may be compelled to simply select the dose regimen that looks numerically “best”, but I see this as analogous to choosing black or red on the roulette wheel based on the result of the last spin; it is painfully unscientific and unsound.
11.1 Example of a Weak Dose-Response Design and Analysis
A real example of the challenges with interpreting data from small trials and narrow dose ranges in oncology is discussed in this section. It includes some observations on Project Optimus, the FDA initiative to reform the dose optimization and dose selection paradigm in oncology. To be useful, the material is necessarily detailed in places, and hence the reader may wish to skip this section.
The following example shows the willingness to interpret results for individual doses levels can be misleading both to the drug company and the regulator. As stated above, we should both “think” and analysis all data from all doses/trials simultaneously via suitable D-E-R models. This provides us with the most accurate and honest understanding of the true D-E-R relationships, and hence the best evidence base to make informed decisions. However consider the following trial called DESTINY-LUNG02 (NCT04644237), where two dose levels of trastuzumab deruxtecan (T-DXd) were investigated for the treatment of HER2-mutated Metastatic Non-Small Cell Lung Cancers (NSCLC). The two dose levels were 5.4 mg/kg and 6.4 mg/kg, and the FDA has granted accelerated approval. Selected text is shown below from the following source:
“T-DXd was evaluated at a 6.4 mg/kg dose across multiple trials and at a 5.4 mg/kg dose in a randomized dose-finding trial. Response rates were consistent across dose levels. Increased rates of interstitial lung disease/pneumonitis were observed at the higher dose. The efficacy results of the approved recommended dose of 5.4 mg/kg given intravenously every 3 weeks are described below.”
“Of the 52 patients in the primary efficacy population…”
“The confirmed objective response rate was 58% (95% confidence interval [CI] = 43%–71%) ”
“This application used advice from the FDA Oncology Center of Excellence (OCE) Project Optimus to conduct a dose-randomization study, which led to a lower dose being approved. For more information regarding the OCE’s efforts to modernize dose selection for oncology products, refer to Project Optimus.”
A parallel trial called DESTINY-LUNG01 [NCT03505710] only considered the 6.4 mg/kg dose in 91 patients, it reported a high rate (46%) of grade 3 or higher drug related adverse events [2]. It stated:
“The safety profile was generally consistent with those from previous studies; grade 3 or higher drug-related adverse events occurred in 46% of patients, the most common event being neutropenia (in 19%)”
To be clear, I am neither an expert in NSCLC nor aware of the unmet need in this patient population. However as a drug developer, there is so much here that looks highly questionable from a dosing justification perspective, and how the limited data collected is being interpreted. The response rate in DESTINY-LUNG02 of 58% would seem to equate with 30/52 patients achieving the objective response, thus we have very few patients. The text proposes that the “response rates were consistent across dose levels”, but the sample sizes are far too small to draw any meaningful conclusions (we should not be guessing!). It also states that the lower dose (5.4 mg/kg) had a (numerically) better safety profile and, based on this, the lower dose was approved by the FDA. The label will now report the results for the 5.4 mg/kg dose. With such small N, and two doses levels that are so close to each other, such interpretations of the relative efficacy and safety of these two doses is highly speculative at best, and simply pure guesswork at worst. Whilst it is perfectly reasonable that the efficacy profile at the two doses were numerically in the same ballpark, and that the safety for 5.4 mg/kg did look numerically better than the 6.4 mg/kg dose, there is a substantial risk we are trying to make informed decisions around the dose regimen based on weak data that is incapable of being used for such decisions. Why is there a risk to the regulator (and patients)? Imagine I am an unscrupulous drug developer, and I want my label to look as good as possible. Under the cloak of supporting Project Optimus, I use 4 doses that are all very close (e.g. 5.4 mg/kg, 5.7 mg/kg, 6.0 mg/kg and 6.4 mg/kg). By having such similar doses and small N, I am essentially maximising my chances that one looks “optimal” by chance, and better than it would truly be. I can get a label based on my “lucky” regimen, although a truly well designed trial (with a very wide dose range) and integrated D-E-R analysis would put these dose levels at broadly similar levels of efficacy/safety. It is analogous to using 5 different shades of blue pills into a trial, and then subsequently seeking approval for the darkest blue pill, since the observed data for that shade of blue happened to look best when compared to the other shade of blue pills.
As an aside, everything above has focussed on a fixed-dose regimen for trastuzumab deruxtecan that is “personalised” using only body weight. In the DESTINY-LUNG01 trial, a total of 88 patients (97%) had drug related adverse events, with 31 patients (34%) having drug-related adverse events that led to dose reduction; 23 patients (25%) discontinued treatment. Drug-related interstitial lung disease occurred in 24 patients (26%), with Grade 1-5 neutropenia (low neutrophil counts (a type of white blood)) being experienced by 32 patients (35%) and Grade 3-5 in 17 patients (19%). A very long list of additional adverse events was reported; this dosing regimen is extremely tough on the patients. The percentage change in tumour dynamics was also reported for each patient, and is reproduced from Li [2] in the Figure 11.2 below.
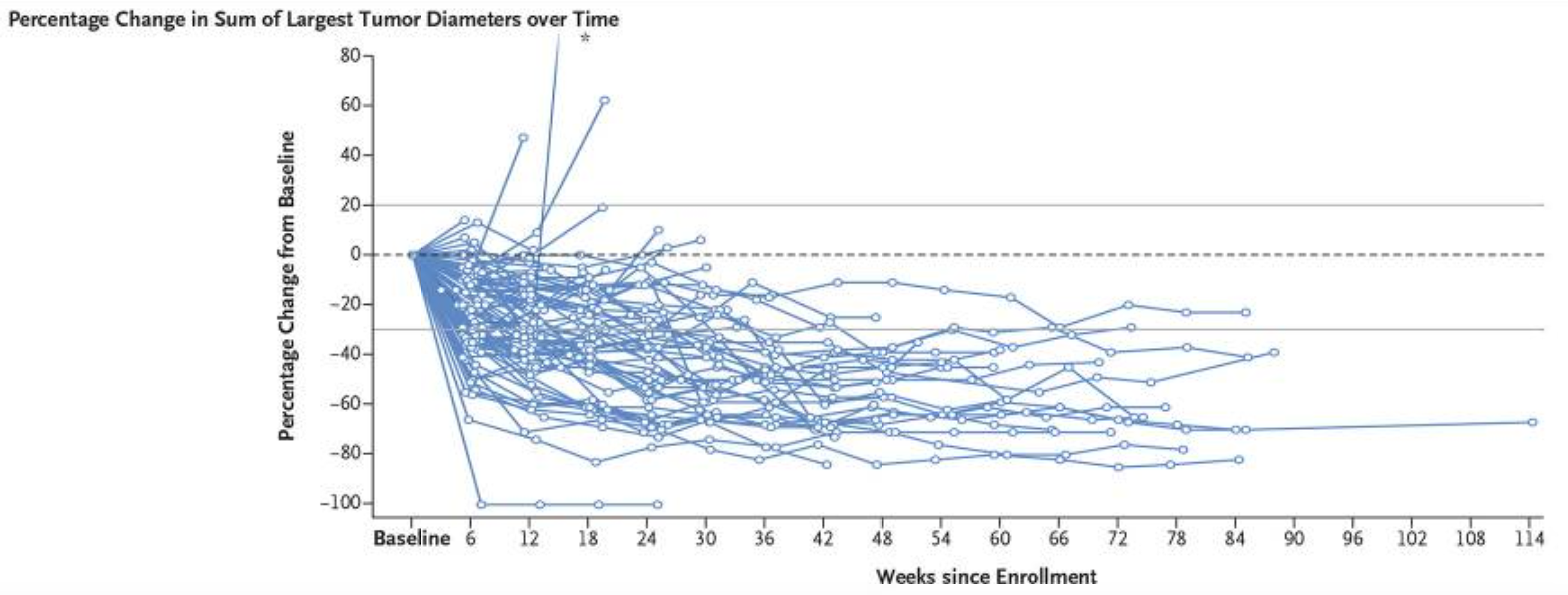
Although these patients all received the same 6.4 mg/kg dose, this figure clearly demonstrates the IIV between patients in a relevant PD endpoint. Following a more comprehensive analysis that looked closely at, for example, the interrelationship between overall survival, tumour dynamics, changes in neutrophil counts and pharmacokinetics, would it not be possible to construct a science-based dose titration algorithm based on, for example, accruing on-treatment data for changes in neutrophil counts, PROs and tumour dynamics? For example, the 17 patients who experienced grade 3-5 neutropenia would not have experienced such severe neutropenia had they started on a lower dose; in our urgency to deliver a very high dose, we are exposing patients to significant toxicities. Is it not important to investigate whether a significant reduction in the tumour diameters can be achieved with lower doses for some patients? Many PKPD models to describe neutrophil counts and predict neutropenia have been developed, so can we not initially titrate the dose to ensure that, at worst, only grade 1 (or 2) neutropenia are observed? Given 25% of patients discontinued treatment in this trial, and the very high number of severe toxicities, are we not ethically compelled to consider such trials? I absolutely think we should be doing better here; intelligently titrating the dose (say over the first 3-18 months) is a small logistical price to pay if we truly care about patients and their outcomes.
In summary, the development of trastuzumab deruxtecan has involved multiple indications beyond NSCLC, so the appropriateness of the dosing regimen proposed in this indication will naturally be augmented by other data. However there is no expert in D-E-R modelling who would consider a dose “range” from 5.4 mg/kg to 6.4 mg/kg as being capable of generating meaningful data for informed D-E-R analysis. The adage “Garbage in, Garbage out” is unfortunately how we need to view such “dose ranging” trials. Before running any such trial, it is essential that clinical trial simulation be used to assess whether the data that will be generated will provide any meaningful quantification of the D-E-R relationships. If such an exercise was performed using doses like 5.4 mg/kg and 6.4 mg/kg in 25-50 patients per arm, I know the virtual trials would show a random collection of outcomes, with 5.4 mg/kg sometimes looking superior to the 6.4 mg/kg arm, with other virtual trials showing the exact opposite. I would argue it is unethical to utilise such a poor design; more informative designs should have been used. Would you agree?
If we truly wish to understand D-E-R relationships, we need appropriate designs and appropriate analysis. In areas outside of oncology, well-designed trials that investigate very wide dose ranges have been successfully used to characterise D-E-R relationships across multiple efficacy and safety endpoints [3] . If Project Optimus is to be truly successful, it must ensure very wide dose range are investigated, and ensure the data from all doses be combined with suitable D-E-R models. Simply advocating a few, closely spaced, dose levels is neither sufficiently informative nor acceptable from either a scientific or patient perspective; we must do much better.